TAChart Tutorial: ColorMapSeries, Zooming/fi
│
English (en) │
suomi (fi) │
Johdanto
"Mandelbrotin joukko", nimetty Benoît Mandelbrotin mukaan, on niin sanottu "fraktaali" -- kaksiulotteinen muoto, joka on tunnettu siitä että se on itsesimilaarinen eri mittakaavoissa. Fraktaalin suurentaminen paljastaa pienimuotoisia yksityiskohtia joka ovat samanlaisia kuin laajamittaiset ominaisuudet. Tässä opetusohjelmassa käytetään TAChart-komponenttia piirtämään Mandelbrot joukon värikarttakuvaajan avulla ja käytetään erilaisia zoomausta tekniikoilla, kuten zoomausta vetämällä tai asettamalla extent historia. Kuten tavallista, tämä vaatii perustiedot työskennellä TAChart-komponentin kanssa jonka perustiedot saadaan kun käydään läpi "Aloitus" opetusohjelma . Ja tietenkin, pitää olla perustiedot Lazarus IDE:stä ja Object Pascal kielestä.
Värikarttakuvaajan (TColormapSeries) käyttö
Mikä on TColorMapSeries?
Normaalisti työskennellään kuvaajien kanssa jotka sisältävät kaksiulotteista dataa - yhdellä akselilla on X- koordinaatit ja toisella y:n arvot, jotka on määritetty x:n arvojen suhteen.
Värikarttakuvaaja (TColorMapSeries) on tästä poikkeus: se näyttää kolmiulotteista dataa : meillä on piste xy ja kolmas arvo, sen korkeus joka liitetään xy-tasoon.
Usein 3D pisteitä, katsotaan kuin vuoria maiseman yläpuolella, pohjan tasossa. Valitettavasti TAChart ei voi piirtää 3D-näkymiä. Mutta on olemassa vaihtoehto: korkeus, alustan tason yläpuolella voi voidaan kuvata värillä, tämä tarkoittaa että kaavio täyttää xy-tason väreillä, jotka vastaavat kolmannen tason koordinaatteja.
Värikarttakuvaaja (TColorMapSeries) on funktionaalinen kuvaaja, mikä tarkoittaa sitä että se ei voi piirtää mielivaltaista dataa, vaan dataa, jotka voidaan laskea funktiona.
Tätä tarkoitusta varten kuvaajalla on tapahtuma OnCalculate jota kutsutaan jokaisen (x, y) pisteelle siirtämään funktion arvo. Tässä mielessä TColorMapSeries on samanlainen kuin funktiokuvaaja (TFuncSeries) jonka käyttöä opetettiin toisessa opetusohjelmassa .
Toinen "perusraaka-aine" on ColorSource joka kuvaa funktion arvot värin. Tähän tarkoitukseen on kätevä käyttää TListChartSource-komponentti. Yleisesti, se tallentaa x ja y:n arvojen kanssa väriarvon ja kuvaavan etiketin TChartDataItem, mutta värikarttakuvaajaa varten tarvitaan vain x- ja väri merkintöjä.
Valmis aloittamaan?
Luo uusi projekti ja lisää client-aligned TChart-komponentti. Älä tee ikkunasta liian suurta, koska tämän opetusohjelman projekti vaatii paljon laskentaa ja suuri määrä pikseleitä heikentää suorituskykyä ...
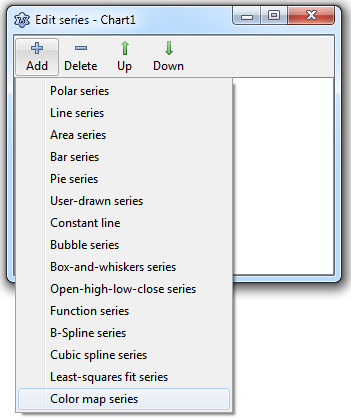
Kaksoisklikkaa kaaviota avataksesi "muokkaa kuvaajia" ikkunan ja lisää "Värikarttakuvaaja" kaavioon. Seuraavaksi pudota TListChartSource lomakkeelle. Tämä on värin lähde Värikarttakuvaajalle (ColorMapSeries). Joten, nimeä se "ColorSource" ja liitä se vastaavaan omaisuuteen kuvaajassa.
Värikarttaan tutustuminen
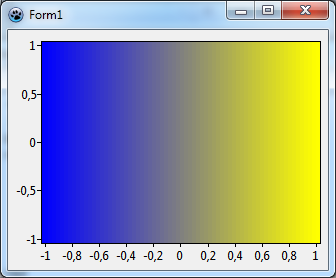
Jotta saadaan joitakin perehtyneisyyttä tästä uudesta ympäristöstä, voidaan aloittaa tekemällä yksinkertainen esimerkki: käytetään värikarttakuvaajaa piirtämään liukuvärjäys x-akselille.
Aluksi kirjoitetaan ColorMapSeries:n tapahtuman käsittelijä OnCalculate. Tämä on helppoa, koska halutaan vain yksinkertainen lineaarinen gradientti eli liukuvärjäys:
procedure TForm1.Chart1ColorMapSeries1Calculate(const AX, AY: Double;
out AZ: Double);
var
ext: TDoubleRect; // unit TAChartUtils.pas
begin
ext := Chart1.GetFullExtent;
AZ := (AX - ext.a.x) /(ext.b.x - ext.a.x);
end;
Jotta ollaan riippumattomia kaavion koosta normalisoidaan x-koordinaatti alueelle x datat ( graph units). X alue voidaan laskea kaavion FullExtent - tämä on suorakulmio kaksinkertaisen tarkkuuden arvot on määritelty kulmassa oleva kaavion piirtämällä suorakulmio ennen kuin zoomausta tai panorointia tehdään. Normalisoituminen kuten yllä varmistaa, että AZ on 0 vasemmalla ja 1 oikealla x-akselin lopussa.
Lopuksi täytyy täyttää ColorSource asetus liukuvärjäyksellä. Tämä on erittäin helppoa, koska ColorMapSeries tekee kaikki interpoloinnit jos sen omaisuus Interpolate asetetaan arvoon true.
Likuvärjäyksen määrittely aloitetaan arvosta 0,0 ja se määritetään siniseksi väriksi. Lopussa liukuvärjäys vastaa arvoa 1,0 ja sen pitäisi näkyä keltaisena. Nämä tehtävät tehdään aliohjelmassa PopulateColorSource jota kutsumme OnCreate lomakkeen tapahtumassa; käytämme erillisessä aliohjelmaa, koska joitakin muutoksia tehdään koko tämän opetusohjelma ajan ja haluataan pitää asiat erillään.
procedure TForm1.FormCreate(Sender: TObject);
begin
PopulateColorSource;
end;
procedure TForm1.PopulateColorSource;
const
DUMMY = 0.0;
begin
with ColorSource do begin
Add(0.0, DUMMY, '', clBlue); // 0.0 --> sininen
Add(1.0, DUMMY, '', clYellow); // 1.0 --> keltainen
end;
end;
Johtuen TListChartSource.Add syntaksista täytyy antaa arvoja y-koordinaatille ja marks tekstille, käytetään siihen vakiota DUMMY ja tyhjää merkkijonoa koska niitä tarvita.
Ajetaan ohjelma. Jos ei nähdä liukuvärjäystä niin ehkä on unohtunut aktivoida ColorMapSource:n Interpolate asetus. Jos hyvin tarkkaan katsotaan niin nähdään joitakin värisävyjen kapeita ryhmittelyjä erityisesti keskustan siirtymäalueella. Tämä johtuu ColorMapSource:n ominaisuuksista StepX ja StepY jotka ovat edelleen niiden oletusarvossa 4. Tämä tarkoittaa sitä, että xy-tasoa ei tarkisteta pikseli kerrallaan, vaan 4x4 pikselin lohkoissa, tämä nopeuttaa piirtämistä. Asetamalla nämä arvoon 1 päästään eroon ryhmittelystä. Parantunut tarkkuus on myös edullista Mandelbrot joukolle myöhemmin. Kuitenkin se hidastaa ohjelman suoritusta, joka voi olla varsin dramaattista, jos on hidas tietokone ...
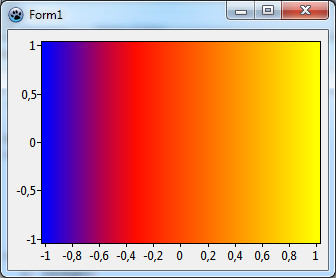
Mennään pidemmälle ja lisätään toinen pivot liukuvärjäykseen. Entä punainen keskellä vastaamaan vaikkapa 0,3? Laitetaan toinen kutsu Add osaksi PopulateColorSource aliohjelmaa. Koska interpolointi vaatii lajitellun luettelon kannattaa lisätä uusi väri muiden väliin tai sitten pitäisi kutsua Sort väriä-arvo-parien lisäämisen jälkeen. Tuloksena on edellä esitetty kolmivärinen liukuvärjäys, käytämme sitä, kun tehdään Mandelbrotin joukkoa.
procedure TForm1.PopulateColorSource;
const
DUMMY = 0.0;
begin
with ColorSource do begin
Add(0.0, DUMMY, '', clBlue); // 0.0 --> sininen
Add(0.3, DUMMY, '', clRed); // 0.3 --> punainen
Add(1.0, DUMMY, '', clYellow); // 1.0 --> keltainen
end;
end;
Mandelbrotin joukko
Joten mikä on Mandelbrotin joukko? Karkeasti ottaen se on joukko pisteitä xy-tasolla jotka noudattavat tiettyä sääntöä, kuten ympyrä, jonka sääntö on, että kaikki ympyrän pisteet(esim joukon) on oltava samalla etäisyydellä origosta.
Niin Mandelbrotin joukon sääntö on vähän monimutkaisempi. "Kompleksinen" maailma on ymmärrettävä tässä kaksitahoissa mielessä: monimutkainen merkityksessä "monimutkainen", mutta myös monimutkainen matemaattisessa mielessä, että kohtia xy käsitellään kuten kompleksilukuja. Jos et ole perehtynyt kompleksilukuihin, älä anna periksi - vältämme täysin laskelmat näillä "oudoilla" numeroilla.
Laskeminen
Paras tapa ymmärtää Mandelbrotin joukko on tehdä sen rakenne. Käytetään seuraavaa reseptiä jokaiselle 2d pisteelle xy tasolla; Näistä lähtöpisteitä on kutsutaan c = (cx, cy).
- Aloita liittämällä c toiseen pisteeseen z = (zx, zy) = (cx, cy).
- Laske z:n "neliö" seuraavalla kaavalla: z2 = (zx2 - zy2, 2 * zx * zy) - tämä kaava voi näyttää hieman oudolta, mutta jos on perehtynyt Kompleksinumeroihin niin huomataan, että se on tapa, miten lasketaan kompleksiluvun neliö. (Jos ei ole perehtynyt niin pidä se annettuna.)
- Lisää sitten c:n koordinaatit c kuin
z2. Tämän seurauksena vaihe on z2 + c = (zx2 - zy2 + cx, 2 * zx * zy + cy) - Nyt otetaan tämä tulos ja laitetaan se vaiheen 2 laskuun jälleen uutena z:n arvona
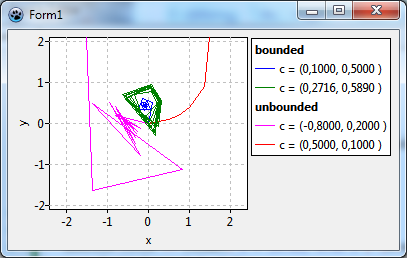
- Toista tämä aliohjelma uudestaan ja uudestaan. Tämän seurauksena piste z seuraa jonkinlaisen lentoradan xy tasossa. Kuvassa näytämme muutamia esimerkkejä, jotka jäljittää:
- Punainen ja fuksia käyrät lopulta siirtää pois alkuperä, nämä polut ovat "rajaton" ("unbounded"). Voidaan osoittaa, että kun polku on ylittänyt kriittisen etäisyyden 2 päässä alkuperää se ei koskaan palaa takaisin ja välttyy äärettömyyteen. Yleensä laskenta laskee toistojen kunnes etäisyys origosta on yli 2. Iteraatioiden lukumäärä on kartoitettu värillä, jota käytetään piirtämän pikselin lähtöpisteestä c.
- Sininen polku, toisaalta, suppenee kohti alkuperää. Vihreä käyrä ei lähentyvät, mutta pysyy paeta säteellä. Molemmat tapaukset ovat nimeltään "rajoitettujen" ("bounded"). Iteratiivinen laskenta menisi loputtomiin. Siksi se pysäytetään iteraatioiden maksimimäärään. Lähtöpisteet c näille liikeradoille sanotaan kuuluvan Mandelbrotin joukkoon ja piirretään mustalla värillä.
Vaikka tämä kuvaus voi kuulostaa vähän hankalalta niin vain muutama rivi Pascal koodia tarvitaan laskennassa. Seuraava funktio määrittää, onko piste c Mandelbrotin joukossa vai ei. Se palauttaa tarvittavien iteraatioiden määrän ja pisteen koordinaatit kun viimeinen iteraatio on suoritettu.
const
MANDELBROT_NUM_ITERATIONS = 100;
MANDELBROT_ESCAPE_RADIUS = 2.0;
MANDELBROT_LIMIT = sqr(MANDELBROT_ESCAPE_RADIUS);
function InMandelbrotSet(c:TDoublePoint; out Iterations:Integer; out z: TDoublePoint): Boolean;
var
j: Integer;
begin
Iterations := 0;
z := DoublePoint(0.0, 0.0); // unit TAGeometry.pas
for j:=0 to MANDELBROT_NUM_ITERATIONS-1 do begin
z := DoublePoint(
sqr(z.X) - sqr(z.Y) + c.X,
2 * z.X * z.Y + c.Y
);
if sqr(z.X) + sqr(z.Y) > MANDELBROT_LIMIT then begin
Result := false;
// point did escape --> c ei kuulu Mandelbrotin joukkoon
exit;
end;
inc(Iterations);
end;
Result := true;
end;
Piirtäminen
Nyt haluamme piirtää Mandelbrotin joukon. Tiedät mitä tehdä? Kyllä - täytyy kirjoittaa vastaava käsittelijä OnCalculate. Tapahtumakäsittelijässä kutsutaan funktiota InMandelbrotSet. Jos piste siirtyi tapahtumakäsittelijän on Mandelbrotin joukkoon asetaan sen väri mustaksi, jos ei niin jaetaan toistojen määrän suurimman iteraatioiden määrällä ja saadaan arvo väliltä 0 ja 1, joka on vastaava merkintä meidän ColorSource . Oh - mutta miten antaa Mandelbrotin joukon mustan värin pisteitä? Lisätään vain uusi numero ColorSource väripariksi joka yhdistää clBlack:n esimerkiksi -1.
procedure TForm1.PopulateColorSource;
const
DUMMY = 0.0;
begin
with ColorSource do begin
Clear;
Add(-1.0, DUMMY, '', clBlack); // -1.0 --> musta
Add(0.0, DUMMY, '', clBlue); // 0.0 --> sininen
Add(0.3, DUMMY, '', clRed); // 0.3 --> punainen
Add(1.0, DUMMY, '', clYellow); // 1.0 --> keltainen
end;
end;
procedure TForm1.Chart1ColorMapSeries1Calculate(const AX, AY: Double;
out AZ: Double);
var
iterations: Integer;
z: TDoublePoint;
begin
if InMandelBrotSet(DoublePoint(AX, AY), iterations, z) then
AZ := -1
else
AZ := iterations / MANDELBROT_NUM_ITERATIONS;
end;
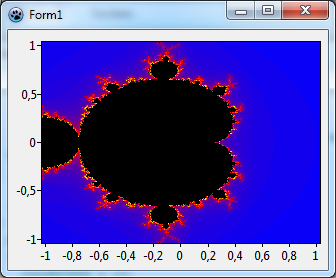
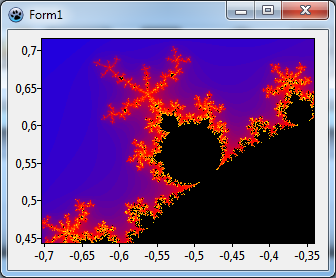
Ja se, mikä on tämän tuloksena - katso vasen kuva:
Erittäin kiva. Mutta kuten tavallista niin ensimmäinen tulos ei ole vielä paras mahdollinen. Tässä kaksi kohtaa, joita voidaan parantaa:
- Kuva on leikattu. Tämä johtuu siitä, ettei määritelty laskennassa x:n ja y:n aluetta mitä ColorMapSeries käyttää. Yleisesti Mandelbrotin joukko nähdään parhaiten, kun x:n arvot ovat välillä -2,2 ja 0,8, sekä vastaavasti y:n arvot ovat välillä -1.5 ja 1.5. Kirjoita nämä numerot kaavion
Extent:n kenttiinXMin, XMax, YMinjaYMaxsekä aseta kentätUseXMin, UseXMax, UseYMinjaUseYMinarvoontruejotta nämä akselien raja-arvot aktivoidaan. Voidaan yhtä hyvin käyttää kuvaajanExtentominaisuutta, mutta sitten pitäisi asettaa kaavionMarginsarvoon 0, ei-täytetyn taustan poistamiseksi lähellä akseleita.
- Kuva näyttää jotenkin vääristyneeltä, jos sitä verrataan kuviin [1]. Tämä tapahtuu, koska x ja y-akselilla on eri yksikköpituudet. Vääristymisen välttämiseksi 0:n ja 1:n välinen etäisyys on oltava yhtä suuri molemmille akseleilla. Tietenkin voidaan alustaa lomakkeen leveys ja korkeus oikein, mutta käyttäjä voi muuttaa sen muotoa, ja se vääristäisi kuvaa uudelleen. Kuitenkin
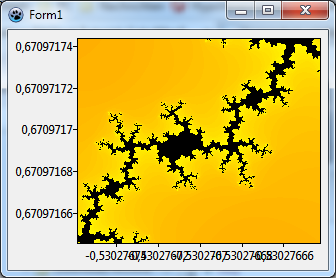
TChart-komponentilla on käytännöllinen ominaisuus ota käyttöön "neliö" koordinaatisto: asetaProportionalarvoontrue. Tällä asetuksella laajuutta x- ja y-akselit säätyy automaattisesti aina samankokoiseen yksikköön.
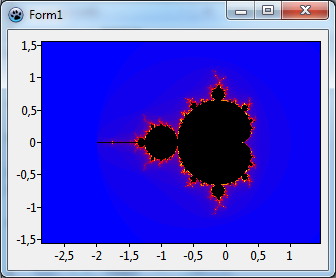
Tulos näiden muutoksien jälkeen näkyy yläpuolella oikeassa kuvassa. Siinä voidaan huomata, että x-akselin alue on laajempi kuin oli pyydetty. Tämä on seurausta Proportional asetuksesta koska kuvasuhde ei ole ikkunassa yhteensopiva miten x- ja y-alueet asetetaan kaavion Extent ominaisuudessa.
Ennen kuin jatketaan opetusohjelmaa, niin "kotitehtävänä" voisi olla tälläinen : Muuta ohjelma niin, että Mandelbrotin joukko ei ole musta, mutta näyttää etäisyyden mukaan värit liikeradan origosta kun iterointi keskeytetään.
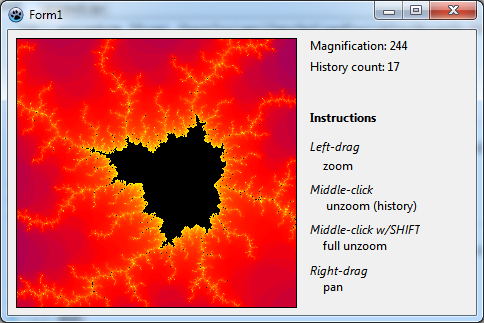
Zoomaus ja vieritys
Johdannossa mainittiin, että Mandelbrotin joukko on itsestään samanlainen kuin suurennetussa mittakaavassa. Tämä näkeminen edellyttää zoomausta - ja tämä tehdään opetusohjelman seuraavassa osassa.
Sisäänrakennettu zoomaus
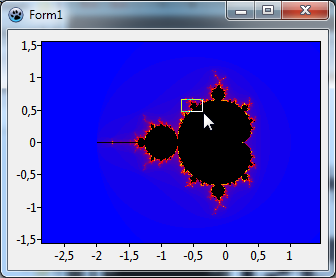
TChart komponentissa on sisäänrakennettuna zoomaus ominaisuudet. Täytyy vain vetää suorakulmio hiirellä ylhäältä-vasemmalta oikeaan alakulmaan alueelle, jota halutaan suurentaa ja pitää hiiren vasenta painiketta alhaalla, vetäessä. Palauta alkuperäinen näkymä vetämällä johonkin toiseen suuntaan tai klikkaa kuvaa.
Tietenkin voidaan käyttää uutta suurennettua kuvaa zoomata siitä uudestaan ja uudestaan. Kuitenkin jossain zoomaustasolla, akselitunnukset pitenevät ja voi lopulta olla päällekkäisiä. Tämä ei näytä hyvältä. Tarvitsemmeko akselit ollenkaan? Ei - ne saadaan pois päältä menemällä komponenttimuokkaimessa vasemmalle ja ala akselille ja asettamalla niiden omaisuus Visible arvoon false.
Mutta ehkä pitäisi olla joitakin viitteitä koosta näyttöikkunassa. Käytössä olevan suurennuksen voidaan näyttää TLabel-komponentilla. Jotta tilaa tulisi muillekin info teksteille myöhemmin tässä opetusohjelmassa, lisätään TPanel komponentti niitä varten. Kohdista tämä "info paneeli" oikealle (Align arvoon alRight) ja poista sen Caption. Jotta saadaan riittävän suuri kaavion uudelleen pitänee muuttaa lomakkeen kokoakin. Lisää label paneelin yläosaan ja nimeä se LblMagnification.
Extents
Miten saada nykyinen suurennus? Näkymä kuvataan TAChart useilla "extents":llä nämä ovat suorakulmioita kuin TRect, mutta kulman pisteet on annettu liukulukuina. Tämä data on tyypiltään TDoubleRect ja se on määritelty käännösyksikössä TAChartUtils. Esillä on jo ollut funktio GetFullExtent on TChart joka palauttaa zoomattoman / vierittämättömän näkymän. Zoomauksen tai vierityksen jälkeinen näkymä saadaan CurrentExtent tai LogicalExtent ominaisuuksilla. Molemmat ovat suorakulmioita ja hyvin samankaltaisia mutta ensinmainittu on hieman suurempi kuin jälkimmäinen, koska se huolehtii myös tarvittavan tilan akselin merkinnöille ja sisemmät kaavio marginaalit. Koska tämä ylimääräinen tila ei oteta huomioon täysimääräisesti, täytyy verrata leveydet full extent / looginen extent ja laskea suurennus. Korkeuksia ei tarvitse miettiä, koska Proportional on asettu kaavion.
On huomattava, että ulottuvuudet (extent) annetaan aina graph unit:na, eli alla olevaan kaavion koordinaatistoon. Koska emme käytä TChartTransformations niin tämä on sama kuin systeemin koordinaatisto näyttäisi akselit (akselikoordinaatit).
Milloin päivitetään suurennusteksti? Aina kaavion koossa (extent) tapahtuu muutoksia. TChart tarjoaa kaksi tapahtumaa tässä kohdassa: OnExtentChanged ja OnExtentChanging. Molemmat tapahtumat syntyvät kun koko on jo muuttunut, OnExtentChanged kutsutaan piirustuksen rutiinin sisällä, OnExtentChanging kutsutaan ennen piirtämistä. Ero on tärkeää, jos tapahtumakäsittelijä aloittaisi uudelleen piirtää kaavion jälleen - tämä voi lukita sovelluksen ... Tässä sovelluksessa ero ei ole merkittävä, joten valitaan OnExtentChanging.
procedure TForm1.Chart1ExtentChanged(ASender: TChart);
var
cex, fex: TDoubleRect;
factor: double;
begin
cex := Chart1.CurrentExtent;
fex := Chart1.GetFullExtent;
if cex.b.x = cex.a.x then exit;
factor := (fex.b.x - fex.a.x) / (cex.b.x - cex.a.x);
if factor > 1e6 then
LblMagnification.Caption := Format('Magnification: %.0e', [factor])
else
LblMagnification.Caption := Format('Magnification: %0.n', [factor]);
end;
Tämä on eräs mahdollinen tapahtumakäsittelijän versio. Koska hyvin suuri suurennuskertoimia on vaikea lukea niin siirrytään käyttämään suurennuksen mennessä yli yhden (1) miljoonan eksponentiaalista numeerista merkintätapaa.
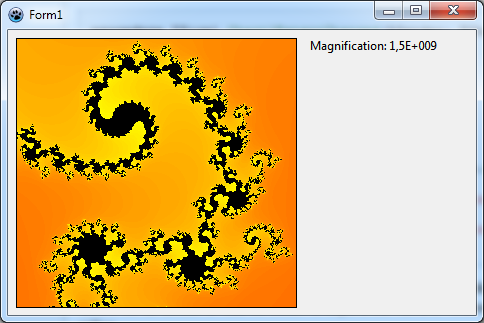
Zoomaus kohti ääretöntä ...
Kokeillaan suurennoksia - kuva oikealla suurennettu yli yhden (1) miljardin kerran (1E9). Ja on mahdollista löytää paikkoja, joissa voit suurennoksia on 1E14 kertaa ennen kuva on "ruma". Jos mietitään tätä numeroa: jos alkuperäinen ei-zoomattu ikkuna olisi 10 cm poikkipituudeltaan - niin tällä suurennuksella se olisi mitattuna 1E13 metriä. Tämä vastaisi kooltaan koko aurinkokuntaa! Ei ole järkevää zoomata enempää, koska me saavuttaneet TAChart sisäisesti käyttämän kaksinkertainen tarkkuuden rajan. Kuitenkin teoriassa, se voi mennä ja ja ...
Kaavion muokkaustyökalujen käyttö
Jos halutaan siirtää näkymää hieman vasemmalle tai oikealle samalla suurennuksella niin Tätä kutsutaan vierittämiseksi tai panoroinniksi. Kuvan vierittäminen onnistuu vetämällä sitä hiiren oikealla painikkeella. Lazaruksen versiossa 1.0 ei ollut sisäänrakennettua vieritys tukea. Mutta siihenkin sen voi tehdä kaavion muokkaustyökaluilla.
Tässä ei mennä yksityiskohtiin, mitä kaavion muokkaustyökalut (ChartTools) ovat ja mitä niillä voi yleensä tehdä. Katso sen opetusohjelmaa jos ne eivät ole tuttuja.
Aloituksessa lisätään ChartToolSet komponentti lomakkeelle ja linkitetään sen ominaisuus Toolset kaavion. Sitten kaksoisklikkaamalla ChartToolSet komponenttia avautuu muokkaustyökalut-ikkuna ja valitaan lisää-painikkeen "takaa" "vieritys vetämällä". Valitse työkalu komponenttimuokkaimessa - se on lapsi ChartToolset objekti puussa - ja asettaa sen ominaisuus Shift arvoon ssRight. Tämä on hiiren painike joka aktivoi vieritystoiminnan. Voidaan yhdistää myös muita avaimia Shift ominaisuuteen, jos halutaan.
Koska sisäänrakennetut työkalut ovat pois päältä kun käytetään ChartToolset:a niin voidaan myös palauttaa zoomaus valmiudet. - Aivan sama tapa: lisää "Zoomaus vetämällä" ja aseta sen Shift ominaisuus arvoon ssLeft.
Jos suoritat ohjelman nyt voit vierittää näkymää vaikka sinulla olisi vanha Lazarus versio.
Zoomaus historia
Jos zoomata syvemmälle ja syvemmälle Mandelbrotin joukkoa voit mennä yhden tai useamman vaiheen takaisin tutkia yksityiskohtia, jotka eivät enää näy nykyisellä zoomaustasolla. Zoom-historia tallentaa kaikki ulottuvuudet, jotka kerran olivat aktiivisia läpi koko zoomaus- ja vieritysprosessissa.
Käännösyksiköiden TATypes ja TAChartUtils tarjoavat luokan TAChartExtentHistory mikä sallii toteuttaa zoomaus historian. Koska tämä ei ole komponentti niin on käytettävä koodia. Se luodaan FormCreate ja tuhotaan FormDestroy tapahtumassa koska zoomaus historia tarvitaan koko ohjelman ajan:
procedure TForm1.FormCreate(Sender: TObject);
begin
PopulateColorSource;
Chart1ColorMapseries1.ColorSource := ColorSource;
// Tämä on uutta:
ZoomHistory := TChartExtentHistory.Create;
ZoomHistory.Capacity := 100;
// Historia voi kaapata 100 kertaa, kunnes vanhin tieto katoaa
end;
procedure TForm1.FormDestroy(Sender: TObject);
begin
ZoomHistory.Free;
end;
Aina zoomauksen tai vierityksessa tapahtuvat näkyvän näkymän muutokset kaaviossa lisätään historiaan. Aloitetaan zoomaus jossa käytetään ZoomDragTool:n tapahtumaa AfterMouseUp yksinkertaisuuden vuoksi. Olisi myös mahdollista käyttää OnExtentChanged tapahtumaa, mutta tässä on oltava varovainen jottaa ohittaa extent muutokset kun perutaan zoomaus (unzooming) - Tästä tarkemmin TAChart mukana olevassa extent demo:ssa.
Huomaa, että extent jo on muuttunut, kun AfterMouseUp tapahtuma tulee. Näin ollen, lisätään historiaan kaavion PrevLogicalExtent - tämä on näkymä, joka oli aktiivinen ennen kuin extent:ä muutettiin:
procedure TForm1.ChartToolset1ZoomDragTool1AfterMouseUp(ATool: TChartTool;
APoint: TPoint);
begin
ZoomHistory.Add(Chart1.PrevLogicalExtent);
end;
Vieritys on vähän mutkikkaampi, koska siinä tapahtuu extent muutoksia liikuttaessa hiirtä. MouseUp hetkellä PrevLogicalExtent joka on aktiivisena vierityksen alkaessa on jo korvattu useita kertoja. Mutta ratkaisu on yksinkertainen: Tässä voidaan käyttää PanDragTool:n OnAfterMouseDown tapahtumaa.
Olisi kiinnostavaa näyttää infopaneelissa myös montako tasoa on otettu muistiin. TChartExtentHistory on sitä vastaava ominaisuus Count . Joten, lisätään toinen teksti ("LblHistoryCount") on infopaneeliin ja muuttaa kaavion OnExtentChanged tapahtumaa lisäämällä seuraava rivi:
LblHistoryCount.Caption := Format('History count: %d', [ZoomHistory.Count]);
Ja miten palautetaan zoomauksen edellinen taso? Lisäämällä yksi CharTTool lisää. Sen käyttöön ei ole mitään erityisiä vaatimuksia, joten otamme UserDefinedChartTool. Aseta sen Shift ominaisuus niin, että työkalu reagoi vain hiiren keskimmäisellä painikkeella. Ja OnAfterMouseClick tapahtumakäsittelijässä luetaan viimeinen kohde historiasta (ZoomHistory.Pop) ja litetään saatu extent suorakulmio kaavion LogicalExtent kohtaan joka säätää näkymän vastaavasti. Tieto poistetaan historiasta pinon lukemisen jälkeen. Historian tietojen määrän näyttö infopaneelissa päivittyy automaattisesti, koska tapahtuma OnExtentChanged tapahtuu. Huomaa, että meidän täytyy tarkistaa onko historiatiedot tyhjänä jolloin vältetään poikkeus.
procedure TForm1.ChartToolset1UserDefinedTool1AfterMouseUp(ATool: TChartTool;
APoint: TPoint);
begin
if ZoomHistory.Count > 0 then
Chart1.LogicalExtent := ZoomHistory.Pop;
end;
Jos halutaan nopeasti palata alkuperäiseen näkymään (suurennuksella 1) voi vetää hiiren vasemmalla painikkeella muuhun suuntaan kuin ylhäältä vasemmalle ja alas oikealle tai vain klikata kaaviota. Koska käyttöön otettiin hiiren keskimmäinen painike zoomauksen perumiseen niin käyttöliittymä voi olla johdonmukaisempi, jos lisätään uusi UserDefinedChartTool ja luovuttaa sen Shift ominaisuutta ssMiddle ja ssShift - usein liitetään ⇧ Shift -näppäin toimintaan jolloin tehdään jotain suurempaa, kuten isoja kirjaimia. Siksi yhdistelmä hiiren keskimmäinen näppäin (zoomauksen peruminen) ja⇧ Shift -näppäin näyttää alkuperäisen näkymän.
Käyttäjän voi kuitenkin olla vaikeaa pitää mielessä kaikki keskeiset yhdistelmät. Siksi lisätään infopaneelin muutamia tekstejä, jossa annetaan ohjeita zoomaukseen, vierittämiseen ja zoomauksen perumiseen.
Niin, tässä on lopputulos tästä opetusohjelma projektista. Pidä hauskaa!
Lähdekoodi
Tämän opetusohjelman lähdekoodi löytyy TAChart:n kansiosta tutorial\mandelbrot.
project1.lpr
program mandelbrot;
{$mode objfpc}{$H+}
uses
{$IFDEF UNIX}{$IFDEF UseCThreads}
cthreads,
{$ENDIF}{$ENDIF}
Interfaces, // this includes the LCL widgetset
Forms, main, tachartlazaruspkg
{ you can add units after this };
{$R *.res}
begin
RequireDerivedFormResource := True;
Application.Initialize;
Application.CreateForm(TForm1, Form1);
Application.Run;
end.
main.pas
unit main;
{$mode objfpc}{$H+}
interface
uses
Classes, ExtCtrls, StdCtrls, SysUtils, TAGraph, TAFuncSeries,
TASources, Forms, Controls, Graphics, Dialogs, TATypes, TATools, Types;
type
{ TForm1 }
TForm1 = class(TForm)
Chart1: TChart;
Chart1ColorMapSeries1: TColorMapSeries;
ChartToolset1: TChartToolset;
ChartToolset1PanDragTool1: TPanDragTool;
ChartToolset1UserDefinedTool1: TUserDefinedTool;
ChartToolset1UserDefinedTool2: TUserDefinedTool;
ChartToolset1ZoomDragTool1: TZoomDragTool;
ColorSource: TListChartSource;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
LblMagnification: TLabel;
LblHistoryCount: TLabel;
Panel1: TPanel;
Panel2: TPanel;
Panel3: TPanel;
procedure Chart1ColorMapSeries1Calculate(const AX, AY: Double;
out AZ: Double);
procedure Chart1ExtentChanged(ASender: TChart);
procedure ChartToolset1PanDragTool1AfterMouseDown(ATool: TChartTool;
APoint: TPoint);
procedure ChartToolset1UserDefinedTool1AfterMouseUp(ATool: TChartTool;
APoint: TPoint);
procedure ChartToolset1UserDefinedTool2AfterMouseUp(ATool: TChartTool;
APoint: TPoint);
procedure ChartToolset1ZoomDragTool1AfterMouseUp(ATool: TChartTool;
APoint: TPoint);
procedure FormCreate(Sender: TObject);
procedure FormDestroy(Sender: TObject);
private
ZoomHistory: TChartExtentHistory;
procedure PopulateColorSource;
end;
var
Form1: TForm1;
implementation
{$R *.lfm}
uses
StrUtils,
TAChartUtils, TAGeometry;
const
MANDELBROT_NUM_ITERATIONS = 100;
MANDELBROT_ESCAPE_RADIUS = 2.0;
MANDELBROT_LIMIT = sqr(MANDELBROT_ESCAPE_RADIUS);
function InMandelBrotSet(
AC: TDoublePoint; out AIterations: Integer; out AZ: TDoublePoint): Boolean;
var
j: Integer;
begin
AIterations := 0;
AZ := DoublePoint(0.0, 0.0);
for j := 0 to MANDELBROT_NUM_ITERATIONS - 1 do begin
AZ := DoublePoint(
Sqr(AZ.X) - Sqr(AZ.Y) + AC.X,
2 * AZ.X * AZ.Y + AC.Y);
if Sqr(AZ.X) + Sqr(AZ.Y) > MANDELBROT_LIMIT then
// point did escape --> AC is not in Mandelbrot set
exit(false);
AIterations += 1;
end;
Result := true;
end;
{ TForm1 }
procedure TForm1.FormCreate(Sender:TObject);
begin
PopulateColorSource;
ZoomHistory := TChartExtentHistory.Create;
ZoomHistory.Capacity := 100;
end;
procedure TForm1.FormDestroy(Sender: TObject);
begin
ZoomHistory.Free;
end;
procedure TForm1.Chart1ColorMapSeries1Calculate(
const AX, AY: Double; out AZ: Double);
var
iterations: Integer;
z: TDoublePoint;
begin
if InMandelBrotSet(DoublePoint(AX, AY), iterations, z) then
AZ := -1
// or - as a solution to the "homework" exercise:
// AZ := sqrt(sqr(z.x) + sqr(z.y)) / MANDELBROT_ESCAPE_RADIUS
else
AZ := iterations / MANDELBROT_NUM_ITERATIONS;
end;
procedure TForm1.Chart1ExtentChanged(ASender: TChart);
var
cex, fex: TDoubleRect;
factor: Double;
begin
cex := ASender.CurrentExtent;
fex := ASender.GetFullExtent;
if cex.b.x = cex.a.x then exit;
factor := (fex.b.x - fex.a.x) / (cex.b.x - cex.a.x);
LblMagnification.Caption :=
'Magnification: ' + Format(IfThen(factor > 1e6, '%.0e', '%0.g'), [factor]);
LblHistoryCount.Caption := Format('History count: %d', [ZoomHistory.Count]);
end;
procedure TForm1.ChartToolset1PanDragTool1AfterMouseDown(
ATool: TChartTool; APoint: TPoint);
begin
Unused(ATool, APoint);
ZoomHistory.Add(Chart1.PrevLogicalExtent);
end;
procedure TForm1.ChartToolset1UserDefinedTool1AfterMouseUp(
ATool: TChartTool; APoint: TPoint);
begin
Unused(ATool, APoint);
if ZoomHistory.Count > 0 then
Chart1.LogicalExtent := ZoomHistory.Pop;
end;
procedure TForm1.ChartToolset1UserDefinedTool2AfterMouseUp(
ATool: TChartTool; APoint: TPoint);
begin
Unused(ATool, APoint);
Chart1.ZoomFull;
end;
procedure TForm1.ChartToolset1ZoomDragTool1AfterMouseUp(
ATool: TChartTool; APoint: TPoint);
begin
Unused(ATool, APoint);
ZoomHistory.Add(Chart1.PrevLogicalExtent);
end;
procedure TForm1.PopulateColorSource;
const
DUMMY = 0.0;
begin
with ColorSource do begin
Clear;
Add(-1.0, DUMMY, '', clBlack);
Add( 0.0, DUMMY, '', clBlue);
Add( 0.3, DUMMY, '', clRed);
Add( 1.0, DUMMY, '', clYellow);
end;
end;
end.
main.lfm
object Form1: TForm1
Left = 326
Height = 285
Top = 155
Width = 468
Caption = 'Form1'
ClientHeight = 285
ClientWidth = 468
OnCreate = FormCreate
OnDestroy = FormDestroy
LCLVersion = '1.1'
object Chart1: TChart
Left = 4
Height = 277
Top = 4
Width = 288
AxisList = <
item
Visible = False
Minors = <>
Title.LabelFont.Orientation = 900
end
item
Visible = False
Alignment = calBottom
Minors = <>
end>
Extent.UseXMax = True
Extent.UseXMin = True
Extent.UseYMax = True
Extent.UseYMin = True
Extent.XMax = 0.8
Extent.XMin = -2.2
Extent.YMax = 1.5
Extent.YMin = -1.5
Foot.Brush.Color = clBtnFace
Foot.Font.Color = clBlue
Proportional = True
Title.Brush.Color = clBtnFace
Title.Font.Color = clBlue
Title.Text.Strings = (
'TAChart'
)
Toolset = ChartToolset1
OnExtentChanged = Chart1ExtentChanged
Align = alClient
BorderSpacing.Around = 4
DoubleBuffered = True
ParentColor = False
object Chart1ColorMapSeries1: TColorMapSeries
ColorSource = ColorSource
Interpolate = True
OnCalculate = Chart1ColorMapSeries1Calculate
StepX = 1
StepY = 1
end
end
object Panel1: TPanel
Left = 296
Height = 285
Top = 0
Width = 172
Align = alRight
BevelOuter = bvNone
ClientHeight = 285
ClientWidth = 172
TabOrder = 1
object Panel2: TPanel
Left = 0
Height = 213
Top = 72
Width = 172
Align = alClient
BevelOuter = bvNone
ClientHeight = 213
ClientWidth = 172
TabOrder = 0
object Label2: TLabel
Left = 6
Height = 13
Top = 8
Width = 69
Caption = 'Instructions'
Font.Style = [fsBold]
ParentColor = False
ParentFont = False
end
object Label1: TLabel
Left = 6
Height = 13
Top = 37
Width = 45
Caption = 'Left-drag'
Font.Style = [fsItalic]
ParentColor = False
ParentFont = False
end
object Label3: TLabel
Left = 6
Height = 13
Top = 80
Width = 53
Caption = 'Middle-click'
Font.Style = [fsItalic]
ParentColor = False
ParentFont = False
end
object Label4: TLabel
Left = 6
Height = 13
Top = 120
Width = 97
Caption = 'Middle-click w/SHIFT'
Font.Style = [fsItalic]
ParentColor = False
ParentFont = False
end
object Label5: TLabel
Left = 6
Height = 13
Top = 161
Width = 51
Caption = 'Right-drag'
Font.Style = [fsItalic]
ParentColor = False
ParentFont = False
end
object Label6: TLabel
Left = 19
Height = 13
Top = 56
Width = 25
Caption = 'zoom'
ParentColor = False
end
object Label7: TLabel
Left = 22
Height = 13
Top = 96
Width = 81
Caption = 'unzoom (history)'
ParentColor = False
end
object Label8: TLabel
Left = 19
Height = 13
Top = 136
Width = 54
Caption = 'full unzoom'
ParentColor = False
end
object Label9: TLabel
Left = 19
Height = 13
Top = 177
Width = 18
Caption = 'pan'
ParentColor = False
end
end
object Panel3: TPanel
Left = 0
Height = 72
Top = 0
Width = 172
Align = alTop
BevelOuter = bvNone
ClientHeight = 72
ClientWidth = 172
TabOrder = 1
object LblMagnification: TLabel
Left = 6
Height = 13
Top = 8
Width = 67
Caption = 'Magnification:'
ParentColor = False
end
object LblHistoryCount: TLabel
Left = 6
Height = 13
Top = 29
Width = 68
Caption = 'History count:'
ParentColor = False
end
end
end
object ColorSource: TListChartSource
left = 115
top = 57
end
object ChartToolset1: TChartToolset
left = 115
top = 120
object ChartToolset1ZoomDragTool1: TZoomDragTool
Shift = [ssLeft]
OnAfterMouseUp = ChartToolset1ZoomDragTool1AfterMouseUp
end
object ChartToolset1PanDragTool1: TPanDragTool
Shift = [ssRight]
OnAfterMouseDown = ChartToolset1PanDragTool1AfterMouseDown
end
object ChartToolset1UserDefinedTool1: TUserDefinedTool
Shift = [ssMiddle]
OnAfterMouseUp = ChartToolset1UserDefinedTool1AfterMouseUp
end
object ChartToolset1UserDefinedTool2: TUserDefinedTool
Shift = [ssShift, ssMiddle]
OnAfterMouseUp = ChartToolset1UserDefinedTool2AfterMouseUp
end
end
end
Samankaltaiset oppimateriaalit
- TAChart opas: Aloitus opas: Ensiaskeleet TAChart-kaaviokomponentilla
- TAChart Tutorial: Chart Tools: johdatus kaaviotyökaluihin (chart tools)
- TAChart opas: Funktiokuvaaja: esittelee
TFuncSeriesjoka seuraa samanlainen käsite kuinTColorMapSeries