Case Compiler Optimization
An editor has declared this article to be a stub, meaning that it needs more information. Can you help out and add some? If you have some useful information, you can help the Free Pascal Wiki by clicking on the edit box on the left and expanding this page.
x86
Jump Table
- Complexity O(1).
Requirements
- 50 or more branches.
- Case labels are not sparse.
Overview
When the number of individual branches grows to a large value, it becomes computationally expensive to test each valid value one-by-one; this is especially the case if a common branch appears at the end of the list (e.g. the largest value of a given set). A jump table seeks to eliminate this penalty by mapping each branch's address into a direct lookup table. Any gaps in the table can easily be filled with an address to the else block (or the end of the case block if one isn't present).
Nevertheless, the lookup table is stored separately to the current code block and must be fetched from memory; this, on top of a near jump, consumes a large number of cycles where the CPU is waiting for the address to reach a register, sometimes to the point where it's faster to simply compare the input contained within a register with each case label individually, since the current block of code is already in the cache and all work is done through immediate values. This is why such jump tables are only beneficial with a large number of branches.
This system, however, breaks down if the range of values is sparse, since this produces an excessively large lookup table where most addresses point to the else block. Even if storage space is not a concern, fetching the lookup table from memory gets more expensive with size.
Example
Say we have a table with 80 entries ranging from -20 to +70, each containing a 32-bit address, with a few values that don't map onto branches redirected to the else block. Since the domain is 90 (70-(-20)), these are indexed sequentially from 0 to 89, with -20 subtracted (i.e. 20 is added) from the input.
Initially, a simple comparison is performed to determine if the input falls within the given range of -20 to +70, and jumps to the else block if not.
sub $-20, %input ; min = -20; this will probably be optimised later to "add $20, %index"
cmp $90, %input ; max-min = 70-(-20) = 90
ja @ElseBlock
This also has the added benefit of remapping %input so the smallest case label is equal to zero.
Even though %input contains a signed value, the design of two's complement notation is taken advantage of because if %input was initially less than -20, then it will still be negative after the remapping, hence the highest bit will be set and will appear to be a very large unsigned number when evaluated under the rules of 'jump if above'. In other words, the JA command successfully branches if %index is too small or too large.
For the actual lookup, it is a simple matter of scaling the input and adding it to the base address of the jump table. For i386:
mov @TableAddress, %addr
add (%addr,%input,4), %addr ; Note: this assumes that the addresses are relative to the base pointer.
; If they aren't, this instruction needs to be "mov" instead
jmp *%addr
For x86_64:
lea @TableAddress(%rip), %base ; 64-bit address.
movs (%base,%input,4), %addr ; Jump addresses are strictly 32-bit, even under x86_64.
add %base, %addr ; Note: this assumes that the addresses are relative to the base pointer.
; If they aren't, this instruction can be removed
jmp *%addr
If size is not a concern, this could be very slightly optimised by having the jump table sign-extended to 64-bit entries, then code similar to the i386 version can be utilised with one fewer registers used:
lea @TableAddress(%rip), %addr
add (%addr,%input,4), %addr ; Note: this assumes that the addresses are relative to the base pointer.
; If they aren't, this instruction needs to be "mov" instead
jmp *%addr
Entire Range Covered
If the entire range of input values is covered, as is the case with an enumerated type, then the initial remapping and range check can be skipped, and all is required is an offset to the reference. For example, if -20 to +70 is the entire valid range:
For i386:
mov %addr, @TableAddress
add -80(%addr,%input,4), %addr ; min*4 = -20*4 = -80
jmp *%addr
For x86_64:
lea %base, @TableAddress(%rip)
movs -80(%base,%input,4), %addr ; min*4 = -20*4 = -80
add %base, %addr
jmp *%addr
Just be warned that this code trusts that the input is sane and isn't set to an ordinal value that is outside of the given valid range (as might happen if the input variable hasn't been initialised). Failure to uphold this prerequisite will cause unpredictable behaviour.
Binary Search Lookup
Main article: Binary search algorithm
- Complexity O(log n)
Requirements
- 32 or more branches.
- All branches call an identical function. Branches that have multiple case values or ranges are treated as individual branches for each single value.
- The range of case labels is large, which would make a direct index or hash lookup impractical.
Most suitable case
A case block that evaluates an ordinal value with many identical branches that share a common header design. Example below taken from compiler\x86_64\aoptcpu.pas, lines 68-119:
{ All subroutines share the form "function(var p: tai): Boolean;" - note that if
one of them is, say "function(const p: tai): Boolean;", this system won't work }
case taicpu(p).opcode of
A_AND:
Result:=OptPass1AND(p);
A_MOV:
Result:=OptPass1MOV(p);
A_MOVSX,
A_MOVZX:
Result:=OptPass1Movx(p);
A_VMOVAPS,
A_VMOVAPD,
A_VMOVUPS,
A_VMOVUPD:
result:=OptPass1VMOVAP(p);
A_MOVAPD,
A_MOVAPS,
A_MOVUPD,
A_MOVUPS:
result:=OptPass1MOVAP(p);
A_VDIVSD,
A_VDIVSS,
A_VSUBSD,
A_VSUBSS,
A_VMULSD,
A_VMULSS,
A_VADDSD,
A_VADDSS,
A_VANDPD,
A_VANDPS,
A_VORPD,
A_VORPS,
A_VXORPD,
A_VXORPS:
result:=OptPass1VOP(p);
A_MULSD,
A_MULSS,
A_ADDSD,
A_ADDSS:
result:=OptPass1OP(p);
A_VMOVSD,
A_VMOVSS,
A_MOVSD,
A_MOVSS:
result:=OptPass1MOVXX(p);
A_LEA:
result:=OptPass1LEA(p);
A_SUB:
result:=OptPass1Sub(p);
A_SHL,A_SAL:
result:=OptPass1SHLSAL(p);
A_SETcc:
result:=OptPass1SETcc(p);
end;
Table Design
Internally, each entry of the lookup table contains two ordinal fields equal to the machine word size, totalling 8 bytes for 32-bit and 16 bytes for 64-bit.
TCaseTableEntry = packed record
Key: NativeInt;
ProcAddr: CodePointer;
end;
TCaseTable = array[0..ListSize-1] of TCaseTableEntry;
The most important element with this table, as with all binary searches, is that it must be sorted by key in ascending order. Given such case tables are static during runtime, this can be done during compilation using any general-purpose sorting algorithm.
Iteration Count
A binary search divides the eligible list in half with each iteration, meaning its complexity grows with the base-2 logarithm of the list size -- that is, the algorithm is O(log n). While this gives us a rough guide as to the number of times the critical loop will run, it is not an exact answer, and log2(n) is only integral when n is a power of 2. However, if we analyse the workings of the binary search, we can deduce the iteration count:
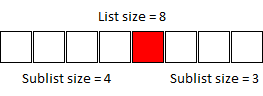
If we take a list size of 8 and evaluate the midpoint (either one of the two middle values will suffice) and determine it is not a match, we can exclude this value and hence are left with one of two sublists to evaluate, one of size 3 and one of size 4. Given the search may take us to the larger of the two, we have to assume worst-case behaviour. Similarly, at size 4, the sublists are of size 1 and 2, and then at size 2, we are left with either a sublist of 1, a match, or a mismatch, since there is no second sublist. At size 1, we just check if this is the value we are looking for, and if not, then we can conclude that the value does not appear in the list.
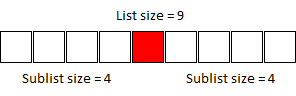
This evaluates to 3 iterations and a final comparison with the 1-sized sublist. This agrees with the value of log2(8) = 3. This is the simplest case though where the list size is a power of two. If we go one higher to a list size of 9...
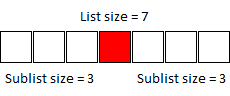
Because we can exclude the midpoint, both sublists have a size of 4, and following the worst-case process listed above, this also results in 3 iterations. If we instead reduce the size to 7...
Both sublists are now only size 3, and taking the midpoint of one of these sublists yields a pair of 1-sized sublists, thereby reducing the iteration count to just 2 plus the final comparison.
From this, we can deduce that the largest sublist size from a list of size n is equal to floor(n/2). Taken to the logical extreme where the sublist size is an odd number in each division stage, we find that only 3 iterations are required up to an initial list size of 15, since this divides down to 7, then 3, and then we are left with one of two 1-sized sublists that just need a comparison. Such number sequences are all 1s in binary, and this corresponds with values of the form 2a - 1, one below the argument that causes log2 to reach its next integral value. Therefore, we can conclude that the total iteration count is a remarkably simple equation:
floor(log2(n))
This is relatively fast to calculate, as it's equivalent to the position of the most significant 1-bit in the binary value of n.
Loop Code
Start with %lo = -1, %hi = number of case labels, %key = value to be searched (assumed to be a signed integer), %table being the address of the map that contains the pointers (which may have to be set beforehand due to the requirement of relocatable code on x86-64), and %mid and %temp undefined. The reason for "lea 2(%lo), %temp" is explained later.
@LoopBegin:
lea 1(%lo,%hi,1), %mid
shr %mid
cmp (%table,%mid,8), %key
cmovge %mid, %lo
cmovle %mid, %hi
lea 2(%lo), %temp
cmp %temp, %hi
jg @LoopBegin
With loop unrolling, this can be simplified further:
lea 1(%lo,%hi,1), %mid
shr %mid
cmp (%table,%mid,8), %key
je @CaseMatch
cmovge %mid, %lo
cmovle %mid, %hi
... with “@CaseMatch” appearing later. This block of code is repeated for each iteration. If there is concern that the conditional jump may incur a performance penalty, it can be removed without incident, especially during the last couple of iterations (an exact match will set %lo and %hi to the same value).
For 64-bit systems, the comparison is more complicated because each entry in the table is 16 bytes, and there is no facility to multiply by 16 in reference operands. Nevertheless, with some rearrangement of the commands to take advantage of a CPU core's multiple ports and the availability of additional registers, this can be resolved relatively painlessly:
lea 1(%lo,%hi,1), %index
lea 1(%lo,%hi,1), %mid
and $-2, %index ; Clear lsb
shr %mid
cmp (%table,%index,8), %key
je @CaseMatch
cmovge %mid, %lo
cmovle %mid, %hi
During the search, the value of %lo is one below the lowest valid index, while %hi is one above the highest valid index. If at any point that %lo + 1 ≥ %hi, the entire list has been searched. Due to how %mid is calculated, if execution passes through the unrolled loop without jumping out, %lo and %hi will have a difference of 2 and sit either side of the index of the last remaining entry in the list that hasn't been checked, hence one final lookup in the table against %key will confirm a match, with a jump to the case's "else" block (or the end of the block if one isn't present) if it's not.
For i386:
lea 1(%lo,%hi), %mid
shr %mid
cmp (%table,%mid,8), %key
jne @ElseBlock
@CaseMatch:
mov 4(%table,%mid,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...
For x86-64 (note the use of %index in the @CaseMatch setion):
lea 1(%lo,%hi), %index
and $-2, %index
cmp (%table,%index,8), %key
jne @ElseBlock
@CaseMatch:
mov 8(%table,%index,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...
Buffer Overrun Trap
One drawback to this highly optimised binary search is that it doesn't trap the situation where the input key is greater than the largest key in the table, and if this happens, the loop may exit with %lo + 1 = %hi = list length, then "lea 1(%lo, %hi), %mid" sets %mid to a value which is out of bounds. To get around this, we recall that in normal operation, %lo and %hi have a difference of 2 if the flow reaches the end of the loop, and are equal if a match was found early, therefore being both odd or both even, their sum is a multiple 2, and so the "+1" part of the LEA instruction has no effect after dividing the sum by 2, so the simple fix is to replace the LEA instruction with "lea (%lo, %hi), %mid", which stops %mid from ever exceeding the upper bound without affecting normal behaviour. In other words, for i386:
lea (%lo,%hi), %mid
shr %mid
cmp (%table,%mid,8), %key
jne @ElseBlock
@CaseMatch:
mov 4(%table,%mid,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...
For x86-64:
lea (%lo,%hi), %index
and $-2, %index
cmp (%table,%index,8), %key
jne @ElseBlock
@CaseMatch:
mov 8(%table,%index,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...
Putting it all together
Now that the registers and exceptional cases are explained, we can put the entire thing together.
For i386:
@LoopBegin:
lea 1(%lo,%hi,1), %mid
shr %mid
cmp (%table,%mid,8), %key
cmovge %mid, %lo
cmovle %mid, %hi
lea 2(%lo), %temp
cmp %temp, %hi
jg @LoopBegin
; Unroll the above if desired
lea (%lo,%hi), %mid
shr %mid
cmp (%table,%mid,8), %key
jne @ElseBlock
@CaseMatch:
mov 4(%table,%mid,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...
For x86-64:
@LoopBegin:
lea 1(%lo,%hi,1), %index
lea 1(%lo,%hi,1), %mid
and $-2, %index ; Clear lsb
shr %mid
cmp (%table,%index,8), %key
cmovge %mid, %lo
cmovle %mid, %hi
lea 2(%lo), %temp
cmp %temp, %hi
jg @LoopBegin
; Unroll the above if desired
lea (%lo,%hi), %index
and $-2, %index
cmp (%table,%index,8), %key
jne @ElseBlock
@CaseMatch:
mov 8(%table,%index,8), %procaddr
; Do common parameter set-up
call %procaddr
; Do common result handling
jmp @CaseBlockEnd
@ElseBlock:
; Else block code
...
@CaseBlockEnd:
...